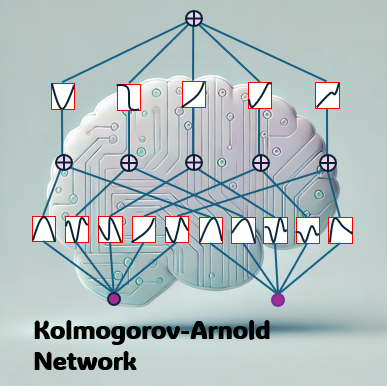
こちらはAX研究室のロベルト・フバチです。この投稿では、比較的新しい種類のニューラルネットワークである コルモゴロフ・アーノルド・ネットワーク（Kolmogorov-Arnold Network, KAN） について紹介します。 その名前はコルモゴロフ・アーノルド表現定理に由来しており、この定理は「任意の多変数関数は1変数関数の和として表現できる」と述べています。
これはどういう意味でしょうか？ たとえ非常に複雑な数学的関係でも、より単純な部分に分解することが可能です。 その結果、理解しやすくなり、処理も容易になります。 そのため、科学者たちは長年この定理に関心を持ち、ニューラルネットワークへの応用を模索してきました。しかし、満足のいく結果を得ることはできませんでした。
転機が訪れたのは2024年4月のことです。この定理を利用したニューラルネットワークの学習方法を説明する論文が発表されました[1]。 それ以来、多くの研究チームがコルモゴロフ・アーノルド・ネットワークに関する研究を発表し始めました [2]。
続きを読む
ニューラルネットワーク
DeepONet：データ駆動型（data-driven）の機械学習による高速シミュレーション
こんにちは、データアナリティクス部門のロベルト・フバチです。
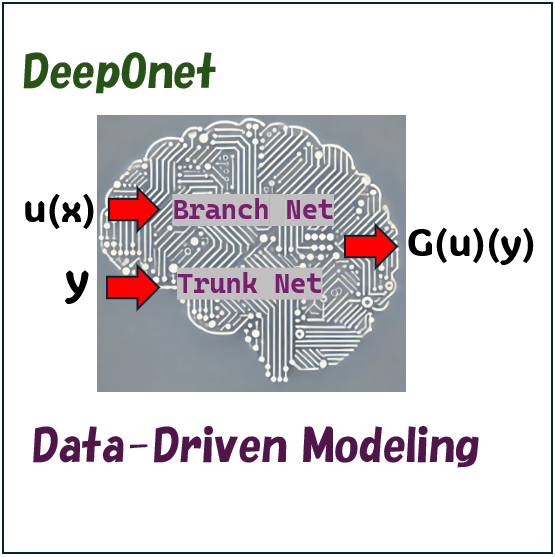
私たちは今、まさに「ビッグデータ時代」に生きています。日々、人々によって膨大なデータが生成・収集されており、これを分析することで貴重な洞察が得られる一方、大きな課題も生まれています。こうした課題に対応するため、新しいツールや技術が次々と登場しています。これにより、データを効率的に処理し、価値ある情報を抽出することが可能になっています。そのツールの一例が、今回のブログで紹介するDeepONet（Deep Operator Network）です。
DeepONetは、ある関数を別の関数に変換する方法を学習するために設計されたニューラルネットワークのアーキテクチャです。従来、このような変換を行うには、2つの関数の関係を定義する明確な規則が必要でした。しかし、DeepONetは与えられた例から直接規則を学習するため、従来のような明示的な規則は不要です。
DeepONetの活用例として、与えられた関数の定積分を計算するタスク（詳細は以下参照）が挙げられます。これは比較的単純なタスクですが、DeepONetはさらに複雑なタスクにも対応可能です。例えば、さまざまなプロセスや自然現象のモデリングが挙げられます。これらのタスクは、しばしば非常に複雑な方程式や規則が関わるため、理解には専門的な知識が求められます。
DeepONetの利点は、複雑な規則をデータから直接学習できる点です。これにより、専門家でなくてもプロセスのモデリングが可能になります。さらに、DeepONetを一度訓練すれば、未知の条件下での問題を従来の方法よりもはるかに速く解決できます。
続きを読む
偏微分方程式を保持したニューラルネットワーク
こんにちはデータアナリティクス部のフバチ(Robert Hubacz)です。以前、偏微分方程式（PDE）を解くための特別なツールである「物理情報ニューラルネットワーク（PINN）」について紹介しました。PDEは自然現象や科学的イベントを理解するのに役立ちます。PINNは少量のデータやデータがなくても機能するため、多くの研究者が関心を持っています。しかし、PINNは一度訓練されると、状況が変わった場合には再訓練が必要です。例えば、パイプ内の水の流れが少し変わるだけでも、PINNを再訓練しなければなりません。一方、未知の状況を予測することは、ニューラルネットワークが作られた主な理由の一つです。
そこで、このブログではPDEを解決するために設計された別のニューラルネットワークについて紹介したいと思います。これらのネットワークは、解決を目指すPDEの構造を反映するように設計されています（Sharma et al., 2023）。具体例として、PDEを保持したニューラルネットワーク（PPNN）というネットワークです（Liu et al., 2024）。
続きを読む
