こちらはAX研究室のロベルト・フバチです。この投稿では、比較的新しい種類のニューラルネットワークである コルモゴロフ・アーノルド・ネットワーク（Kolmogorov-Arnold Network, KAN） について紹介します。 その名前はコルモゴロフ・アーノルド表現定理に由来しており、この定理は「任意の多変数関数は1変数関数の和として表現できる」と述べています。
これはどういう意味でしょうか？ たとえ非常に複雑な数学的関係でも、より単純な部分に分解することが可能です。 その結果、理解しやすくなり、処理も容易になります。 そのため、科学者たちは長年この定理に関心を持ち、ニューラルネットワークへの応用を模索してきました。しかし、満足のいく結果を得ることはできませんでした。
転機が訪れたのは2024年4月のことです。この定理を利用したニューラルネットワークの学習方法を説明する論文が発表されました[1]。 それ以来、多くの研究チームがコルモゴロフ・アーノルド・ネットワークに関する研究を発表し始めました [2]。
KANはどのように構成されていますか？
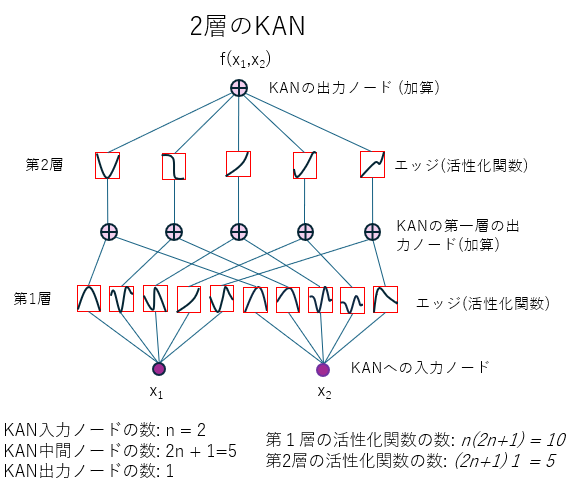図１．最も単純な2層KANネットワークのアーキテクチャ。このネットワークは、コルモゴロフ・アーノルド表現定理に基づいて構築されています。つまり、入力ノードが n 個ある場合、ネットワークには第1層と第2層の間に 2n+1 個のノードがあり、出力には 1 個のノードが存在します。ネットワークの層間にあるノードは、第一層の出力ノードであると同時に、第二層の入力ノードでもあります。図は記事[1]を参考に作成されました。
最も単純な KAN は2層構造になっています（図1参照）。しかし、実際には2層のネットワークでは、あらゆる関数を十分に近似するには不十分です。そのため、通常のニューラルネットワークと同様に、KAN も多層構造を持っています。各 KAN の層は、入力ノード（ニューロン）と、それに接続された出力ノードで構成されます。ノード間の接続は、1変数関数のみを使用する活性化関数（activation functions)によって実現されます。
各層における活性化関数の数は、入力ノード数 × 出力ノード数で決まります。各活性化関数の値は、入力ノードの1つの値のみに基づいて計算されます。その後、これらの関数の値が適切に合計され、出力ノードの値が得られます。このプロセスは、信号が層から層へと伝わる際に繰り返されます。
この仕組みにより、KAN の各層は1変数の関数のみで構成されているにもかかわらず、KAN の出力は、すべての入力ノードの値を使用して計算された多変数関数となります（図1参照）。
では、どのような関数が活性化関数として使用されるべきでしょうか？
実は、KAN は学習データに基づいて、トレーニングの過程で適切な活性化関数を自ら学習します。
この際、KAN はBスプライン（B-splines）と呼ばれる関数近似手法を使用します。これは、関数を小さな部分（セグメント）に分割し、それぞれの部分を特定の形状の関数（例えば3次関数など）で近似する方法です。この関数の形状は数値パラメータによって調整されます。そして、このパラメータの値を学習することが、KAN のトレーニングの目的となります。
また、これらのパラメータは活性化関数の形状を表すため、意味を理解しやすいものです。そのため、従来のニューラルネットワークの学習で使用される解釈が難しい重みパラメータとは異なります。
XAI（説明可能なAI）の例としての KAN
従来のニューラルネットワークは、しばしば「ブラックボックス」と呼ばれます。これらのネットワークは非常に複雑な計算を実行できますが、入力データと計算結果の関係を理解するのは容易ではありません。 これは、ネットワーク内部の情報が重みとして符号化されているためです。重みは単なる数値であり、人間にとって直感的に理解しにくいものです。このため、たとえ精度が高くても、ネットワークの計算結果に対する信頼性が低下することがあります（特に、医療・金融・法律などの分野において [3]）。
これに対して、KAN は知識を活性化関数の形で保存します。これらの関数は可視化できるため、入力データがネットワークの最終出力にどのように影響を与えるかを視覚的に確認することができます。 これにより、KAN の仕組みが理解しやすくなり、従来のニューラルネットワークと比べて透明性が向上します。
さらに、トレーニング後の KAN は、機能性を大きく損なうことなく、小型化（圧縮）することが可能です。 これには「プルーニング（Pruning）」[1] と呼ばれる手法が用いられます。この手法は、機械学習でよく知られる L1 正則化 に基づいています。プルーニングを行うと、ノード間の接続密度が低下し、最も影響力の大きい活性化関数のみが残ります。こうして、小型化された KAN はさらに理解しやすくなります。
プルーニングの後には、追加で「記号回帰（symbolic regression）」[1] を適用することも可能です。これは、活性化関数の形状を最もよく表現する数学的な方程式を見つけるプロセスです。例えば、sin, cos, exp などの基本的な数学関数を用います。
KAN と記号回帰を組み合わせた興味深い応用例として、原子核物理学の研究 [4] があります。この研究では、KAN を活用して、核結合エネルギーを計算するための簡略化された解析式を提案しました。その結果、この式は古典的な物理モデルと一致することが示されました。
まとめ
コルモゴロフ・アーノルドネットワークは、データのモデリングと分析に対する新しいアプローチを提供します。従来のニューラルネットワークとは異なり、KANはより透明性が高く、理解しやすいのが特徴です。その理由は、ネットワークの「知識」が解釈しにくい重みではなく、活性化関数の形で保存されるためです。これにより、研究者やエンジニアはネットワークの意思決定プロセスをより簡単に理解できます。さらに、KANは効果を大きく損なうことなく簡素化し、サイズを縮小することも可能です。この特性により、KANは特にAIモデルの動作を説明することが重要な場面で、有用なツールとなります。
文献：
[1] Z. Liu, Y. Wang, S. Vaidya, F. Ruehle, J. Halverson, M. Soljacic, T. Y. Hou, M. Tegmark: KAN: Kolmogorov–Arnold Networks, arXiv:2404.19756v4
[2] S. Somvanshi, S. Aaqib Javed, M. M.l Islam, D. Pandit, S. Das: A Survey on Kolmogorov-Arnold Network, arXiv:2411.06078
[3] B. Delovski, Kolmogorov – Arnold Networks: The Future of AI?, blog link
[4] H. Liu, J. Lei, Z. Ren: From Complexity to Clarity: Kolmogorov-Arnold Networks in Nuclear Binding Energy Prediction, arXiv:2407.20737v2
