こんにちは、データアナリティクス部門のロベルト・フバチです。
私たちは今、まさに「ビッグデータ時代」に生きています。日々、人々によって膨大なデータが生成・収集されており、これを分析することで貴重な洞察が得られる一方、大きな課題も生まれています。こうした課題に対応するため、新しいツールや技術が次々と登場しています。これにより、データを効率的に処理し、価値ある情報を抽出することが可能になっています。そのツールの一例が、今回のブログで紹介するDeepONet(Deep Operator Network)です。
DeepONetは、ある関数を別の関数に変換する方法を学習するために設計されたニューラルネットワークのアーキテクチャです。従来、このような変換を行うには、2つの関数の関係を定義する明確な規則が必要でした。しかし、DeepONetは与えられた例から直接規則を学習するため、従来のような明示的な規則は不要です。
DeepONetの活用例として、与えられた関数の定積分を計算するタスク(詳細は以下参照)が挙げられます。これは比較的単純なタスクですが、DeepONetはさらに複雑なタスクにも対応可能です。例えば、さまざまなプロセスや自然現象のモデリングが挙げられます。これらのタスクは、しばしば非常に複雑な方程式や規則が関わるため、理解には専門的な知識が求められます。
DeepONetの利点は、複雑な規則をデータから直接学習できる点です。これにより、専門家でなくてもプロセスのモデリングが可能になります。さらに、DeepONetを一度訓練すれば、未知の条件下での問題を従来の方法よりもはるかに速く解決できます。
DeepONetのアーキテクチャ
DeepONet[1]は、2つのサブネットワークで構成されています(図1):
- Branch Net:
選択された点(センサーと呼ばれる)における入力関数𝑢の値を処理します。 - Trunk Net:
出力関数の値を計算する位置情報をエンコードします。
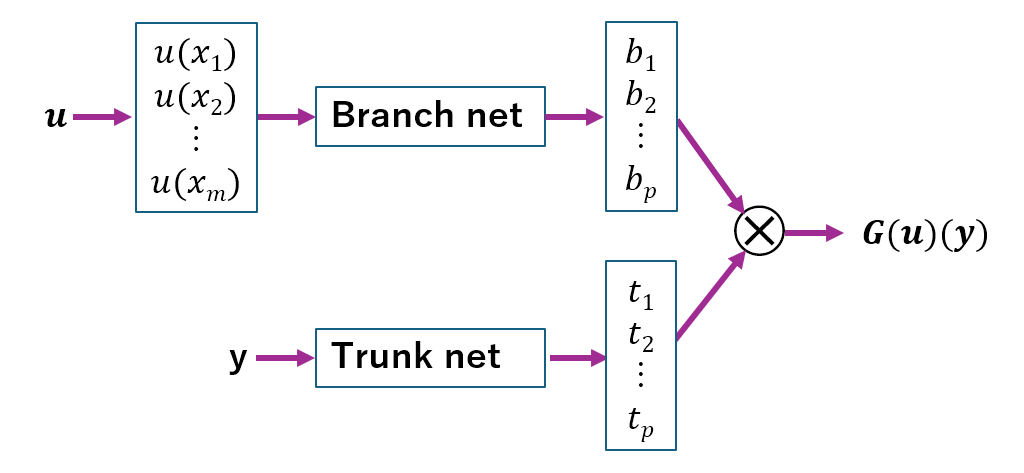
図1.DeepONetのアーキテクチャ。
図1の記号の意味:
𝑢: 入力関数、
𝑥𝑖(𝑖=1,2,…,𝑚): センサー(𝑢の値が計算される点)、
𝑦: 出力関数の値が計算される位置、
t1, t2, . . . , tp: Trunk Netの出力,
b1, b2, . . . , bp: Brunch Netの出力,
𝐺: 関数𝑢に作用する演算子、
𝐺(𝑢)(𝑦): 位置𝑦で計算された出力関数の値 (Trunk NetとBrunch Netの出力の内積)。
DeepONetの訓練中、位置𝑦はセンサーの点によって与えられます。訓練は、予測値と出力関数の真値(ground truth)との差を最小化することで行われます。訓練が完了すると、DeepONetはランダムな位置(つまり、ランダムな𝑦の値)でも出力関数の値を予測できるようになります。
これらのサブネットワークのアーキテクチャには厳格な要件はなく、単純な全結合型ニューラルネットワークで構成できます。しかし、畳み込みネットワークや再帰ネットワークなど、より複雑なアーキテクチャを使用することで、モデルの精度を向上させることが可能です。
DeepONetの動作を説明するために、2つの例を使用する。
例1: 不定積分演算子 (antiderivative operator)
この演算子の厳密な数学的定義には深入りしませんが、単純に言えば「関数の微分の逆操作」を行うものです。したがって、DeepONetの文脈では、この演算子のタスクは、関数𝑢(𝑥)を0から𝑥𝑖まで定積分することと解釈できます([1,2]参照)。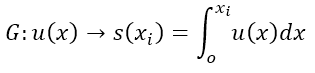
トレーニングデータセットは、区間[0,1]から選ばれた𝑚個の点𝑥𝑖と、多様なタイプや特性を持つ𝑛種類の異なる数学関数𝑢で構成される必要があります。また、各点𝑥𝑖における各関数の定積分の真値(ground truth value)を計算する必要があります。
モデルの入力データ
- 点𝑥𝑖を含む配列(Trunk Netへの入力)
- 各点𝑥𝑖に対する各関数𝑢の値を含む行列(Branch Netへの入力)
モデルの出力
- 関数𝑢の定積分の予測値を格納した行列
トレーニング中、損失関数はモデルが予測した積分値と、事前に計算された真の積分値(ground truth)との差に基づいて計算されます。
例2: 流体のシミュレーション
流体をシミュレーションするには、通常、偏微分方程式のセットを解く必要があります。しかし、DeepONetのデータ駆動型アプローチを用いれば、シミュレーションや実験データが利用可能な場合、これらの方程式を解く必要はありません。
この手法の適用例として、記事[3]で紹介されているパイプ内の流れのシミュレーションを使用します。比較的理解しやすい例であるため、これを選びました。
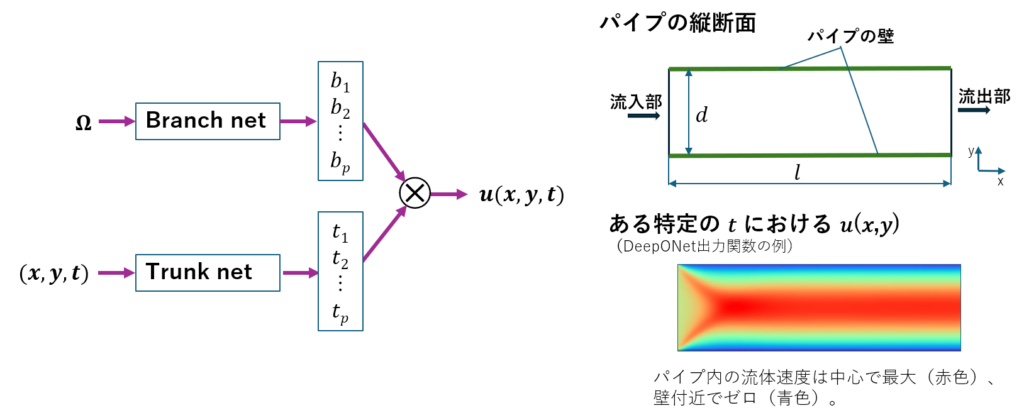
図2. パイプ内の流体の流れのシミュレーション用DeepONetのアーキテクチャ
図2の記号の意味:
Ω: 動作パラメータと形状。動作パラメータは流体の入口速度とその物理的特性(密度と粘度)によって定義され、形状はパイプの長さ(l)と直径 (d)によって定義される。
𝑥,𝑦,𝑡: 時空間座標ベクトル。𝑥と𝑦は空間内の位置(パイプの内部)を示し、𝑡は時間を表す。
𝑢(𝑥,𝑦,𝑡): 特定の位置(𝑥,𝑦)と時間𝑡における流体の速度を示す関数。
この問題でDeepONetを訓練するには、さまざまなΩセットに対する関数𝑢(𝑥,𝑦,𝑡)の情報が必要です。しかし、一度訓練が完了すれば、新しい未知のΩセットに対して、従来の偏微分方程式を解く方法よりもはるかに短い時間で𝑢(𝑥,𝑦,𝑡)を予測できます。
文献:
[1] L. Lu, P. Jin and G. E. Karniadakis.:DeepONet: Learning nonlinear operators for identifying differential equations based on the universal approximation theorem of operators, arXiv:1910.03193
[2] H. Kumar: DeepONet kaggle notebook
[3] Y. Luo, Y. Chen, Z. Zhang:CFDBench: A Large-Scale Benchmark for Machine Learning Methods in Fluid Dynamics,arXiv: 2310.05963




