こんにちはデータアナリティクス部のロバート・フバチです。少し前に、「物理情報ニューラルネットワーク（PINN）」物理情報ニューラルネットワーク）について書きました。このネットワークは、自然界や工業で起きる現象を記述する偏微分方程式を解くために使われます。しかし、このネットワークの欠点は、一度学習させると、その特定の条件に対してのみ解を提供し、新しい条件下での予測には使えないという点です。PINNの学習には、よく数値計算のコンピュータシミュレーション結果 が使われます。これはPINNの可能性を示すためには有用ですが、実用的な観点から見ると、それほどでもありません。既に数値解が得られているので、新しい計算を行う必要がないからです。新しい条件下での予測にも使えるより実用的な方法として、実験や測定結果と組み合わせたPINNが提案されています。そこで、今回はこの活用例を2つ紹介したいと思います。
医療画像用のPINN
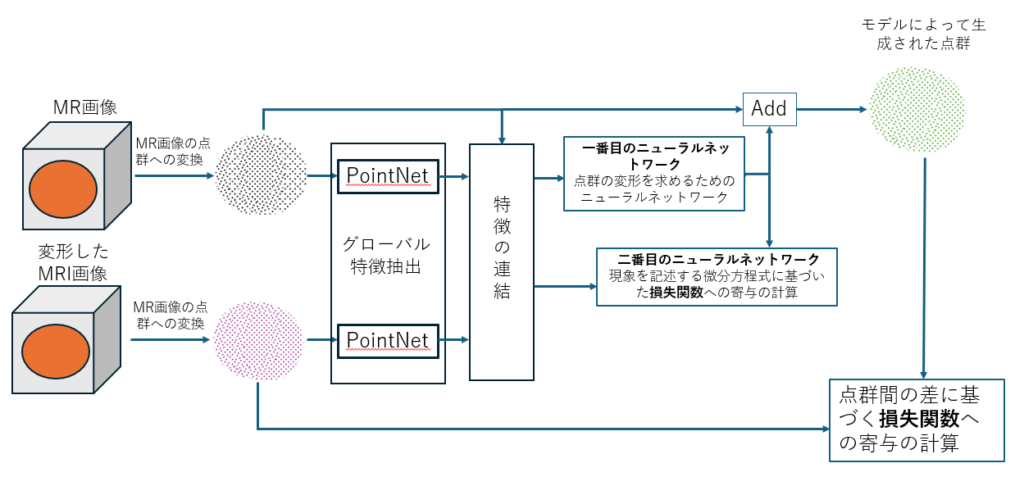
図１．医療画像解析におけるPINNの利用例。図は[1]および[2]に基づいて作成されました。
論文[1]と[2]では、MRIや超音波検査で得られた画像を用いて、人体の臓器の変形を解析するためのPINNの興味深い応用が説明されています（図1にモデルが示されています）。この研究では特に、バイオプシー手術や超音波検査中の圧力によって引き起こされる前立腺の変形に注目しています。超音波やMRIで得られた臓器の画像は、三次元の点群データに変換されます。このモデルには、変形前の臓器を表す点群と変形後の点群の2つが入力されます。これらの点群の特徴を抽出するために、 PointNet というニューラルネットワークが使用されます。
抽出された特徴は、その後2つの別々のニューラルネットワークに送信されます。1つ目のネットワークは臓器の変形を予測し、Chamfer距離が損失関数として使われています。この距離は、実際の点群とモデルによって予測された点群の違いを測定します。2つ目のニューラルネットワークは、弾性理論に基づく物理方程式を使用して変形を説明します。損失関数（物理ベースの損失関数）は、これらの方程式の両側を一致させるように最適化され、物理的に正確な結果を得ることを目指しています。
このモデルは臓器の変形を予測するだけでなく、臓器の特性を診断することにも利用でき、病気の診断に役立つ可能性があります。
PIV補正のためのPINN
論文[3]で説明されているモデルは、産業機器内の液体の流れの速度ベクトルの成分を測定する際の誤差補正やノイズ除去を目的としています。
このケースでは、遠心ファンが対象です。測定は PIV 粒子画像流速測定法）を用いて行われました。
PIVは、非常に小さい粒子を液体に加えることで、その流れを視覚化する方法です。この方法では、専用の光学システムを使用して、装置内の2次元平面内（図2）でこれらの粒子の動きを記録します。それに基づいて、観測された平面内の流体の水平および垂直の速度成分が計算されました。ただし、これらの測定には誤差があり、数値計算結果と比較するとデータに欠損が生じることがあります。したがって、これらの測定には誤差補正が必要です。
著者たちは、測定結果を画像として扱い、その境界は測定が行われた領域の境界に対応していました。この画像の各ピクセルは、液体の流れ速度ベクトルのいずれかの成分を表していました。このようにして、流れ速度の測定結果の補正を画像の再構成として扱うことができました。結果として、PIV法による測定結果の再構成には、畳み込みオートエンコーダー型ニューラルネットワークの使用が提案されました（図2）。
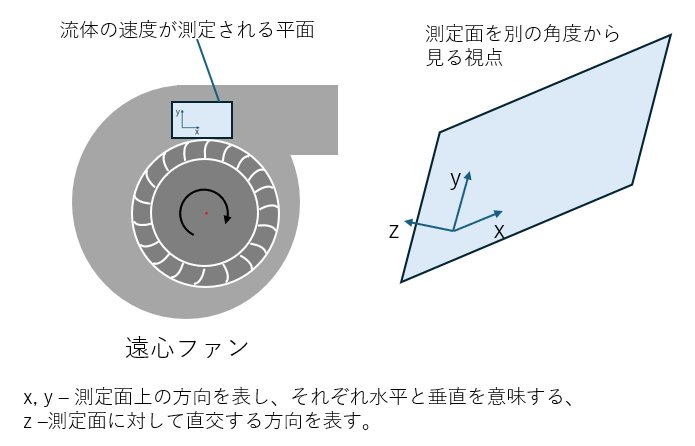
図2．ここでは、遠心ファン、測定面、およびこの平面に対する空間の方向がどのように理解されるかが簡略化して示されています。PIV法を使用して、x方向およびy方向の速度を測定することができましたが、z方向の速度は測定できませんでした。
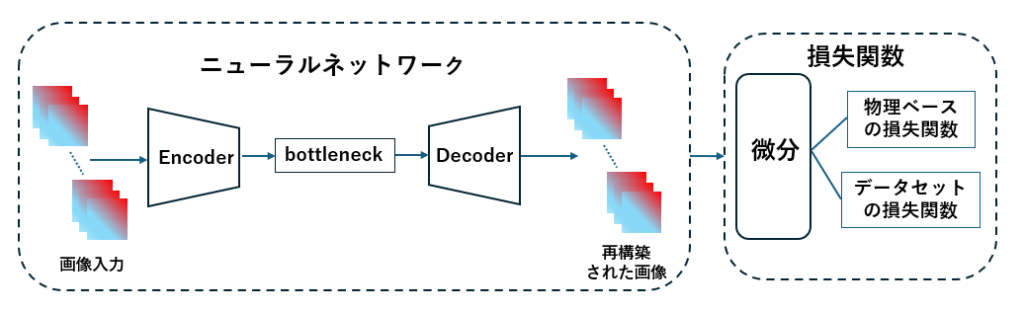
図3．物理インフォームド畳み込みオートエンコーダーの図。微分と記された部分は連続の式で導関数を計算するために使用されます。「画像入力」は測定結果を表し、「再構築された画像」は誤差補正後の測定結果を表しています。図は[3]に基づいて作成されました。
このタイプのニューラルネットワークを訓練するためには、損失関数として、測定時に得られた流体の速度と、ニューラルネットワーク（測定結果を補正した後）の計算によって得られた流体の速度との差の合計を使用するだけで十分です。この方法で算出された損失関数は、データ損失関数と呼ぶことができます （図4）。しかし、データセット損失関数は問題に対して統計的なアプローチを提供するものの、物理法則を考慮していないことが指摘されました。そこで著者たち[3]は、物理法則を考慮した損失関数（物理ベースの損失関数）を追加することを提案しました。このために、連続の式を使用しました。この方程式は、任意の領域を通過する流体の質量が時間とともに変化しないという原則を示しています。つまり、領域に流入する量は、流体の密度が一定である場合、同じ量が流出しなければならないことを意味します。
図4．モデルの損失関数を算出する方法。
この方程式で示されているように、第3の速度成分（図4）が現れましたが、測定中にこれを特定することができませんでした。なぜなら、この成分が測定面に対して直交する方向の流速だからです。しかし、連続の式を使用することで、この速度成分の導関数を簡単に計算することができます。その後、この導関数は損失関数を計算するために使用できます（図4）。
上記のアプローチを使用することで、著者たちはPIV測定結果の再構築の精度を向上させることができました。さらに、補正後の測定結果は、上記で言及された連続の式などの物理法則をより反映していました。また、畳み込みニューラルネットワークを使用することで、連続の式における導関数の計算が簡素化されるという効果もあります。また、一般的に使用される自動微分とは対照的に、畳み込みフィルターは訓練を必要としません。その結果、訓練されたモデルは、測定条件（つまりプロセスの進行状況）が変化した場合にも使用することができます。
文献：
[1] Z. Min, Z.M.C. Baum, S.U. Saeed, M. Emberton, D.C. Barratt, Z.A. Taylor, and Y. Hu (2024): Biomechanics-informed Non-rigid Medical Image Registration and its Inverse Material Property Estimation with Linear and Nonlinear Elasticit, arXiv:2407.03292v2
[2] Z. Min, Z.M.C. Baum, S.U. Saeed, M. Emberton, D.C. Barratt1, Z.A. Taylor, and Y. Hu (2023): Non-rigid Medical Image Registration using Physics-informed Neural Networks, arXiv:2302.10343v1
[3] M. Soltani, G. Akbari, and N. Montazerin (2024): Trade-off between reconstruction accuracy and physical validity in modeling turbomachinery particle image velocimetry data by physics-informed convolutional neural networks, arXiv:2403.00183
