こんにちは。デバイスソフトウエア開発部の斎藤です。
現在新卒2年目で、エッジAIシステム開発、iOSアプリケーション開発を行っています。
今回は、3Dプログラミングの基本的な概念と、SwiftのフレームワークであるARKitとRealityKitでの実装例を紹介しようと思います。
3Dプログラミングの概念は、ARだけでなくゲームやCG・ロボットプログラミングなど様々な分野で登場するので、ARに興味がない方も是非ご一読ください!
3Dプログラミングとは
三次元空間内でのオブジェクトの生成、配置、回転、スケーリング等を行う技術です。
オブジェクトの位置・向き・スケールを表現するために、「座標系」や「クォータニオン」といった概念を使用します。
座標系
SwiftでのARアプリケーションでは、主に以下3つの座標系を使用します。
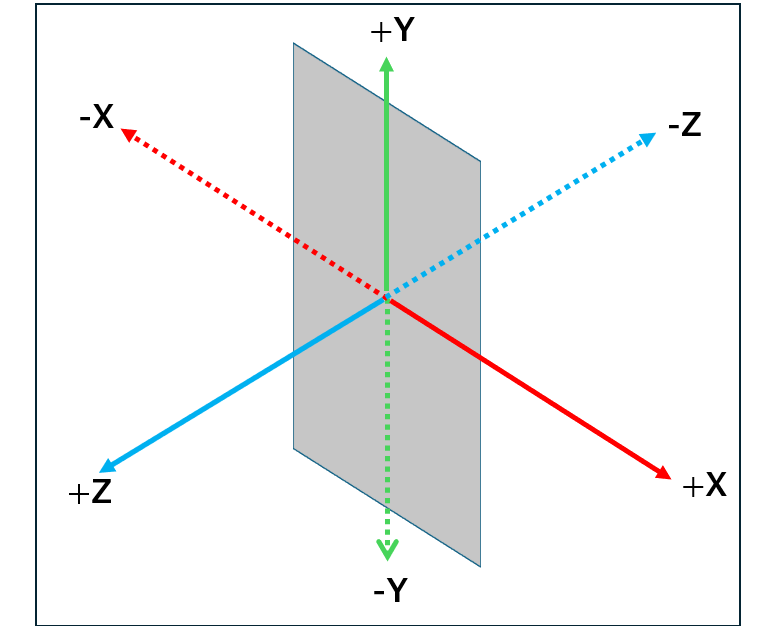
直交座標系
空間をX軸、Y軸、Z軸の3軸で定義し、座標値(x, y, z)で位置を表現します。
ARKitでは、右利きに合わせた右手座標系(Z軸のプラス方向矢印が手前を向く)が採用されています。
余談ですが、ゲーム開発プラットフォームのUnityなどは左手座標系(Z軸のプラス方向矢印が奥を向く)を採用しているそうです。
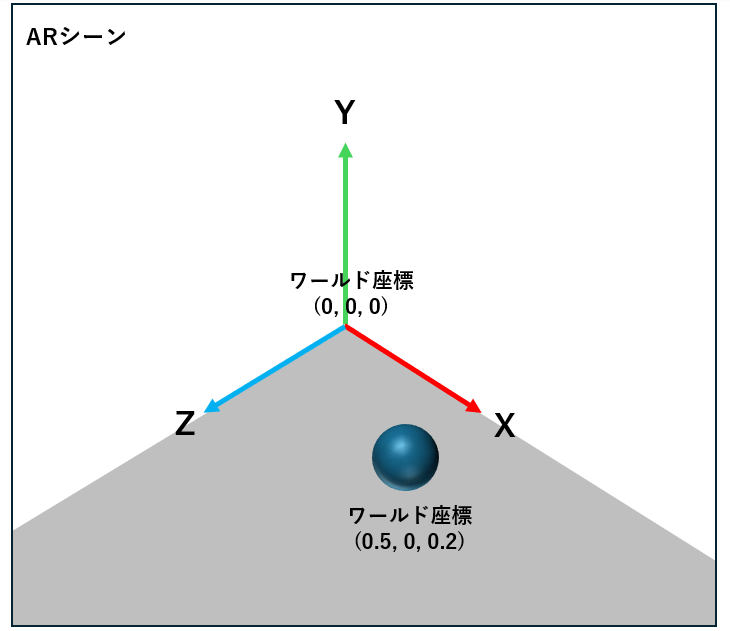
ワールド座標系
全体の基準となる座標系で、オブジェクトの絶対的な位置を表します。例えるなら部屋全体を基準とし、家具を置く位置を指定するようなイメージです。
ワールド座標系を移動させれば、部屋ごと移動する感覚ですべてのオブジェクトが同じ方向に移動します。
ARKitでは、デバイスのカメラが最初に起動されたときの位置をワールド座標の原点(0,0,0)とすることができます。
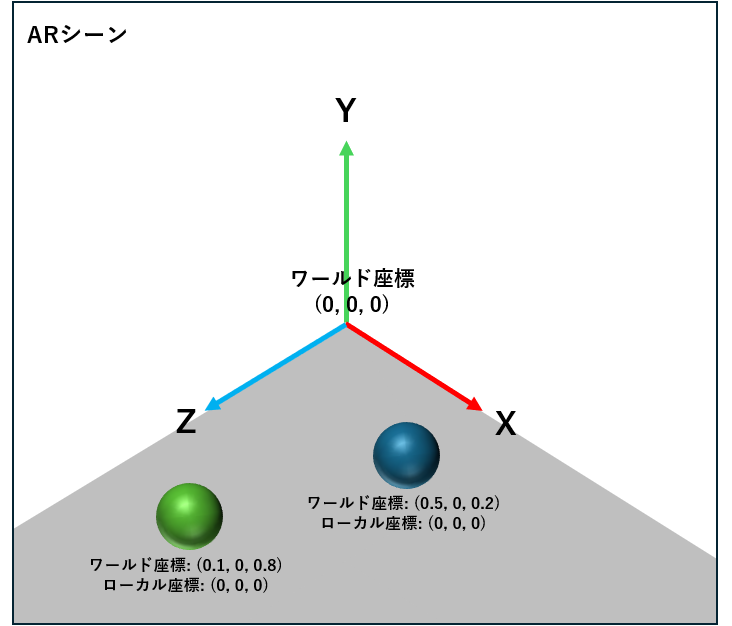
ローカル座標系
生成された各オブジェクトを基準とした座標系で、オブジェクトの相対的な位置や方向を表現します。
1つ1つのオブジェクトが、ワールド座標とローカル座標の2つの座標系情報を保持しているということになります。
クォータニオン(四元数)
3D空間上でオブジェクトの回転を表現するための数学的なツールです。回転の中心に「回転軸(ベクトル)」「角度(スカラー)」の性質を持たせることで、回転操作を直感的に行うことができます。
軸を持つことで「どの方向にむかって回転するか」、角度を持つことで「どれくらい回転するか」を決定できます。
ARKitとは
Apple社が提供する、Swiftで拡張現実(AR)アプリケーションを開発するためのフレームワークです。
iOSデバイス(iPhone, iPad等)のカメラとLiDARセンサーを活用して、現実世界に仮想オブジェクトを重畳表示することができます。
以下がARKitの具体的な役割です。
- カメラとセンサーからデバイスの位置と動きをリアルタイムでトラッキングする。
- 床や水平面を検出し、安定したAR表示を提供する。
- ARセッション(インスタンス)の開始・停止・再開を管理する。
RelityKitとは
同じくApple社が提供する、ARオブジェクトのリッチな3Dレンダリングや物理シミュレーションを開発するためのフレームワークです。
ARKitとセットで使用し、以下のような機能を提供します。
- オブジェクトの影やリアルなグラフィックを表現する。
- 衝突などの物理的な挙動を再現し、リアルな動きを再現する。
- シーン内のオブジェクト(RelityKitではエンティティと呼ばれる)を管理し、属性や挙動を制御する。
ARKitとRelityKitを使用した実装
概念をざっくり紹介したところで、実際にフレームワークでARオブジェクトを設置するサンプルを紹介します。
xcodeのバージョンは15.2、開発デバイスはiPadPro(11インチ)(iPadOSバージョン17.5.1)を使用しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
import SwiftUI import ARKit import RealityKit struct ContentView: View { var body: some View { ARViewContainer().edgesIgnoringSafeArea(.all) } } struct ARViewContainer: UIViewRepresentable { func makeUIView(context: Context) -> ARView { let arView = ARView(frame: .zero) // ARセッション開始 let config = ARWorldTrackingConfiguration() arView.session.run(config) // カメラ位置を基準としたアンカーを作成 let cameraAnchor = AnchorEntity() arView.scene.anchors.append(cameraAnchor) // 立方体モデル作成 let mesh = MeshResource.generateBox(size: 0.1) let material = SimpleMaterial(color: .red, roughness: 0.3, isMetallic: true) let model = ModelEntity(mesh: mesh, materials: [material]) // モデルの位置をカメラから 前方向50cm に設定 model.position = SIMD3(0, 0, -0.5) // カメラ位置基準のアンカーにモデルを追加 cameraAnchor.addChild(model) return arView } func updateUIView(_ uiView: ARView, context: Context) {} } |
上記実装をビルドすることで、世界座標(0,0,0)から前方向に50cmずらした位置に赤い立方体のARオブジェクトを設置することができました。

続いて、関数makeUIViewに以下のコードを追加してクォータニオンを定義し、先ほどのエンティティに適応してみます。
関数simd_quatfに、Z軸を表す(0,0,1)、45度を弧度法で表現したπ/4ラジアンを引数として渡すことでクォータニオンを取得します。
オブジェクトのtransform.rotationプロパティの値をクォータニオンで更新することで、x軸方向に45度回転させています。
|
1 2 3 4 5 6 7 |
// 回転角と回転軸の設定 let angle: Float = .pi / 4 let rotationAxis = SIMD3(0, 0, 1) // クォータニオンを作成 let quaternion = simd_quatf(angle: angle, axis: rotationAxis) model.transform.rotation = quaternion |
ビルドしてアプリを起動すると、以下画像のようにオブジェクトがZ軸を中心に45度回転していることが確認できます。

最後に、設置したオブジェクトのローカル座標系を基準に、右に20cm移動させた位置にオブジェクトを設置してみます。
|
1 2 3 4 5 6 7 8 9 |
// 隣に設置する球体オブジェクト let sphereMesh = MeshResource.generateSphere(radius: 0.05) let sphereMaterial = SimpleMaterial(color: .blue, roughness: 0.3, isMetallic: true) let sphereModel = ModelEntity(mesh: sphereMesh, materials: [sphereMaterial]) // 球体の位置を直方体のローカル座標系に基づいて設定 sphereModel.position = SIMD3(0.2, 0, 0) // 直方体モデルの子として球モデルを追加 model.addChild(sphereModel) |

狙い通り、 立方体のローカル座標系を基準として、右に20cmずらした位置に球体を設置することができました!
おわりに
本記事で紹介したARフレームワークを利用することで、内部的な計算処理を考慮せずにARアプリケーションを実装することが可能です。
しかし、よりユーザビリティが高いアプリケーションを開発するためにはフレームワークを自分で拡張するシーンなども出てくるため、おのずと3Dプログラミングの概念の理解が必要になってくると感じています。
フレームワークの理解・拡張にはクォータニオンの理論(複素数・行列とベクトル)の理解も必要になります。機会があれば、クォータニオンの理論部分とフレームワーク拡張にフォーカスした記事も書いてみようと思いますのでお楽しみに!
エコモットでは、私が現在携わっているAIやARなどを含むモダンな技術を活用したシステム開発に携わるチャンスがたくさんあります!
気になった方はぜひ、下記の採用ページもご覧ください。